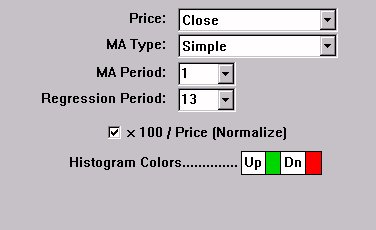
The Linear Regression Slope indicator provides the slope at each bar of theoretical regression lines which involve that bar and the previous N-1 bars (N being the regression period). First, the data, based on the price selected, is smoothed using the moving average period and type (specify a period of 1 if no pre-smoothing is desired). The resulting data is then used to form regression lines ending at each bar, using the regression period specified. The slope of each bars regression line is the recorded as the linear regression slope value for that bar. For instance, assume a MA period of 1 and a Regression Period of 13. The raw closing price would be used and no smoothing performed since the MA period is 1. For each bar, we would then use the price data for that bar and the previous 12 bars (13 total) to form a regression line. The slope of that regression line is then recorded as the indicator value for that bar. The same calculation is done for each bar and then plotted in the chart. The slope can then be optionally normalized. Normalization is discussed in further detail below.
The raw slope essentially gives us the change in price per bar of the regression (best fit) line. If the slope is 1, then the regression line is rising at a rate of $1 per bar. Similarly, a slope of -0.25 would indicator that the line that best fits the last N bars of data is falling at the rate of $0.25 per bar.
If the "x 100 / Price (Normalize)" options is checked, then the resulting value will be divided by 100, and then multiplied by the price of that bar. This normalizes the data for the sake of comparison among instruments that trade in different price ranges. If you are interested in using this study to compare slopes between instruments, it's important that this normalizing option be used. The difference between the normalized slope and the raw slope is similar to the difference between percent change (normalized), and change(unnormalized). If you're comparing two instruments, one that's trading at 200 and another that's trading at 10, then it's not fair to compare the change in price, although the normalized value of percent change does give us a fair basis of comparison.
The normalized slope value essentially gives us the percent change is price per bar of the regression (best fit) line. If the normalized slope is 0.10, then the regression line is rising at a rate of 0.10% per bar. Similarly, a normalized slope of -0.25 would indicator that the line that best fits the last N bars of data is falling at the rate o 0.25% per bar.
The resulting slope is drawn as a histogram that oscillates about 0. A reference line is drawn at the 0 level. A slope that is rising (greater than previous value of slope) is drawn in the up color, while a slope that is falling (lower than previous value of slope) is drawn in the down (dn) color.
See Also
Presentation
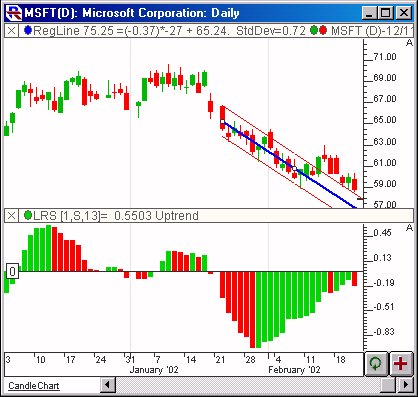
Above is a Daily Candlestick Chart of an Microsoft Corp (MSFT). The histogram in the lower window pane represents the normalized slope using the preferences specified below. A 13-period linear regression line with 2-standard deviation channels is drawn overlaying the candles in the upper pane.
Formula
Keyboard Adjustment
The periods involved in the LRS indicator can be adjusted directly from they keyboard without opening up the preference window. First, select the indicator, then use the up and down arrow keys to adjust the regression period up or down by 1. To adjust the MA period, hold down the shift-key while pressing the up and down arrows.